Tree

그래프의 한종류로써 서로 다른 두 노드를 잇는 길이 하나뿐인 자료구조이다

계층적 관계를 표현하는 비선형 자료구조이다

하나의 root 노드를 가지며 루트 노드는 0개 이상의 자식 노드를 갖고 있다

그 자식 노드들도 0개 이상의 자식 노드를 갖고 있고 이는 반복적으로 정의된다

트리에는 사이클이 존재할 수 없다, 노드들은 특정 순서로 나열될 수도 있고 그럴 수 없을 수도 있다

각 노드는 어떤 자료형으로도 표현 가능하다

용어

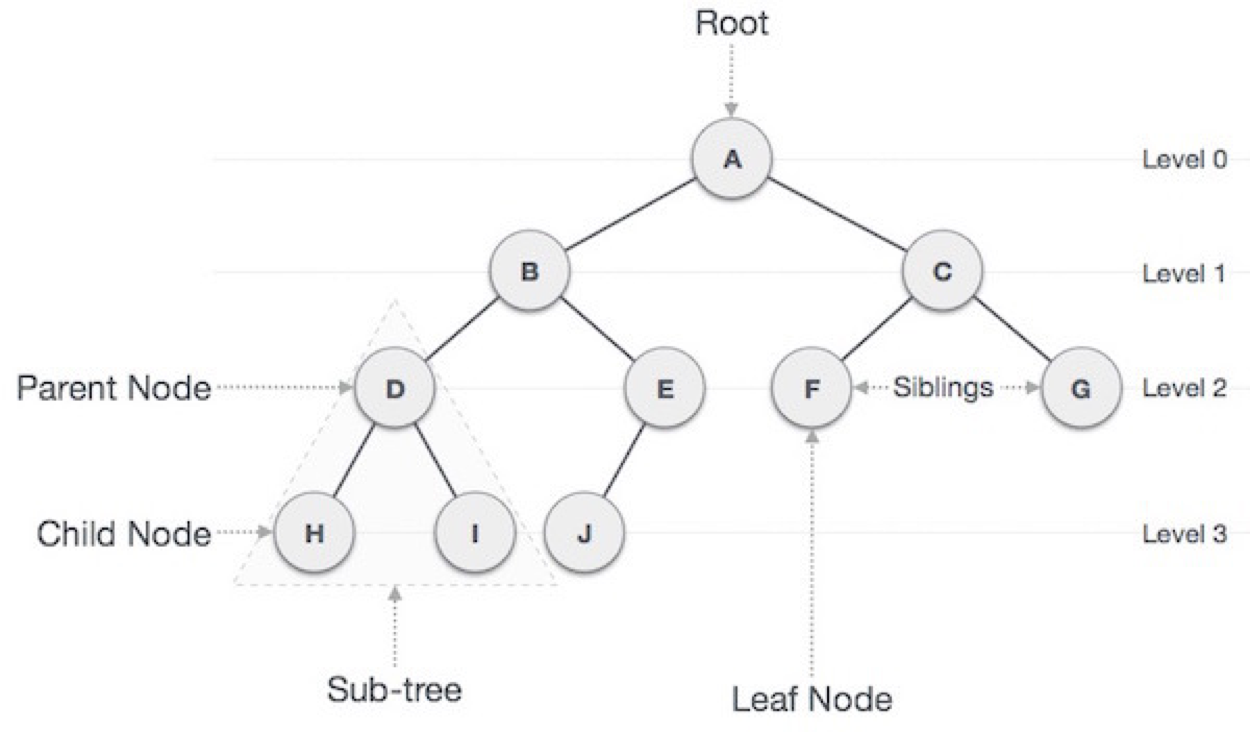
• root node: 부모가 없는 노드, 트리는 하나의 루트 노드만을 가진다.

• leaf node: 자식이 없는 노드

• internal node: leaf node가 아닌 노드

• edge: 노드를 연결하는 선 (link, branch 라고도 부름)

• siblings: 같은 부모를 가지는 노드

• size: 자신을 포함한 모든 자손 노드의 갯수

• depth: 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 edge의 수

• level: 트리의 특정 깊이를 가지는 노드의 집합

• height: root node에서 가장 깊숙히 있는 노드의 깊이

특징

• 노드가 N개인 트리는 항상 N-1개의 edge을 가진다

• root node에서 어떤 노드로 가는 경로는 하나뿐이다

• 한 개의 root node만이 존재하며 모든 자식 노드는 한 개의 부모 노드만을 가진다

이진 트리 종류

완전 이진 트리

완전 이진 트리는 트리의 모든 높이에서 노드가 꽉 차 있는 이진 트리를 말한다 마지막 단계는 꽉 차 있지 않아도 되지만 노드가 왼쪽에서 오른쪽으로 채워져야 한다.

전 이진 트리

전 이진 트리는 자식이 하나만 있는 노드가 존재 하지않는 이진 트리를 말한다

포화 이진 트리

포화 이진 틀리는 전 이진 트리이면서 완전 이진 트리인 경우를 말한다 모든 말단 노드는 같은 높이에 있어야 하며, 마지막 단계에서 노드가 꽉 차 있어야 한다

포화 이진 트리는 노드의 개수가 정확히 nᵏ⁻¹(k는 틀리의 높이)개여야 한다

이진 트리 순회

중위 순회

중위 순회는 왼쪽 가지, 현재 노드, 오른쪽 가지 순서로 노드를 방문하고 출력하는 방법을 말한다.

이진 검색 트리(BST)에서 중위 순회를 하면 O(n)의 시간으로 sort할 수 있다.

function inOrderTraversal(node) {
  if (node !== null) {
    inOrderTraversal(node.left)
    visit(node)
    inOrderTraversal(node.right)
  }
}

전위 순회

전위 순회는 현재 노드, 왼쪽 가지, 오른쪽 가지 순서로 노드를 방문하고 출력하는 방법을 말한다

function preOrderTraversal(node) {
  if (node !== null) {
    visit(node)
    preOrderTraversal(node.left)
    preOrderTraversal(node.right)
  }
}

후위 순회

후위 순회는 왼쪽 가지, 오른쪽 가지, 현재 노드 순서로 노드를 방문하고 출력하는 방법을 말한다

function postOrderTraversal(node) {
  if (node !== null) {
    postOrderTraversal(node.left)
    postOrderTraversal(node.right)
    visit(node)
  }
}

3가지 방법중 가장 빈번하게 사용되는 순회 방식은 중위 순회이다.

이진 탐색 트리

이진 탐색 트리

Graph vs Tree